Noções de probabilidade e estatística: Conceitos Gerais
Como é visto em Editais: Conceitos gerais: variável, tipos de variáveis, população, amostra, frequências: absoluta e relativa, frequências acumuladas, representações em gráficos e tabelas (linhas, colunas, setores e histogramas).
QUESTÕES RESOLVIDAS E COMENTADAS
(instituto access 2024) No que se refere a estatística descritiva, analise e julgue as alternativas.
I. Responsável pela coleta, organização, descrição e resumo dos dados observados.
II. A partir de um determinado conjunto de dados, a Estatística Descritiva busca organizá-los em tabelas (ou gráficos) e estabelecer um sumário por meio de medidas descritivas como a média, os valores mínimo e máximo, o desvio padrão, entre outras.
III. A estatística se divide em três grandes ramos: estatística descritiva (também chamada de indutiva), estatística probabilística, estatística inferencial (também chamada de dedutiva).
: Somente as afirmativas I e II estão corretas.
III - Incorreta. A estatística se divide em três grandes ramos: estatística descritiva, estatística inferencial e probabilidade. Estatística descritiva não é chamada de "indutiva" e estatística inferencial não é chamada de "dedutiva".
INferencial: INdutiva;
DEscritiva: DEdutiva
(fundação cetrede 2024) Uma variável aleatória é uma função que descreve os resultados de um experimento através de valores numéricos. É um exemplo de variável aleatória discreta: Número de ações vendidas de uma empresa.
Na estatística descritiva existem as variáveis que podem ser:
Variável QUALITATIVA nominal: Não tem uma ordenação. Exemplos: sexo (M ou F), profissão (pedreiro, contador, analista)
Variável QUALITATIVA ordinal : Tem uma ordem. Exemplo: Escolaridade (Ensino fundamental, médio, superior), classe social (baixa, média e alta).
Variável QUANTITATIVA discreta: são números inteiros (ex 1, 2, 3). número de filhos (não tem como você ter 1,23 filhos)
Variável QUANTITATIVA contínua: números quebrados (ex 1,247 / 5,78). Exemplos: peso (75,83 kg), altura (1,76 m)
A variável aleatória discreta é aquela que pode assumir um número finito ou infinito contável de valores específicos. Entre as alternativas fornecidas, a variável aleatória discreta seria: Número de ações vendidas de uma empresa.
(fgv 2024) A afirmação que descreve corretamente os conceitos e as relações entre variáveis quantitativas e qualitativas é:
A) variáveis quantitativas podem ser obtidas a partir de variáveis qualitativas em situações particulares;
Em algumas situações específicas, é possível transformar uma variável qualitativa em uma variável quantitativa. Por exemplo, atribuir números a categorias qualitativas pode permitir a análise numérica das mesmas (como em escalas ordinais).
B) variáveis quantitativas são características observadas em populações, enquanto variáveis qualitativas são características observadas em amostras;
Incorreta. Tanto variáveis quantitativas quanto qualitativas podem ser características observadas tanto em populações quanto em amostras. A diferença fundamental entre elas é a natureza da medida (numérica para quantitativas e categórica para qualitativas), não onde são observadas.
C) variáveis quantitativas são características subjetivas, enquanto variáveis qualitativas são características objetivas;
Incorreta. Não há relação direta entre a natureza subjetiva ou objetiva das variáveis e sua classificação como quantitativas ou qualitativas. Ambos os tipos de variáveis podem descrever aspectos subjetivos ou objetivos, dependendo do contexto da medição.
D) variáveis quantitativas são contínuas, enquanto variáveis qualitativas são discretas;
Incorreta. Variáveis quantitativas podem ser contínuas ou discretas, dependendo da natureza da medição. Da mesma forma, variáveis qualitativas podem ser ordinais, nominais ou outras categorias, não se limitando a serem discretas.
E) variáveis quantitativas são representadas por números inteiros.
Incorreta. Variáveis quantitativas podem incluir números inteiros, mas não estão restritas a eles. Elas podem incluir números decimais e outras representações numéricas.
(fgv 2024) A opção que apresenta uma variável qualitativa é:
A) altura;
É uma variável quantitativa contínua, pois pode ser medida em números reais.
B) escolaridade;
É uma variável qualitativa, pois descreve a categoria ou nível de educação alcançado (por exemplo, ensino médio, graduação, mestrado).
C) idade;
É uma variável quantitativa discreta, pois pode ser contada em números inteiros.
D) peso;
É uma variável quantitativa contínua, pois pode ser medida em números reais.
E) salário.
É uma variável quantitativa contínua, pois pode ser medido em números reais.
(fgv 2024) Um pesquisador está estudando a altura dos estudantes de uma universidade. Ele coletou dados e deseja classificar essa variável como discreta ou contínua. A afirmação verdadeira em relação à natureza dessa variável é: a variável é contínua, pois são números reais;
Variável contínua: Uma variável contínua pode assumir qualquer valor dentro de um intervalo, incluindo números reais e frações. A altura é um exemplo clássico de variável contínua, pois pode ser medida com precisão em milímetros, centímetros, metros, etc., e não se limita a valores inteiros.
Variável discreta: Uma variável discreta assume valores distintos e separados, geralmente inteiros. Exemplos incluem o número de alunos em uma sala de aula ou o número de carros em um estacionamento.
(cespe/cebraspe 2024) Variáveis qualitativas são definidas por várias categorias, representando uma classificação dos indivíduos. CERTO
Ex: Estado civil, sexo, raça, cor dos cabelos, nível de instrução, classe social
As variáveis qualitativas se dividem em Nominal e Ordinal.
Variável Nominal é aquela para a qual não existe nenhuma ordenação nas prováveis realizações. Ex.: População: Alunos do Ensino a Distância Variáveis: Sexo, religião, naturalidade, cor, tipagem sanguínea.
A variável ordinal (ORdem) é aquela para a qual existe uma ordem ou hierarquia nos possíveis resultados. Ex.: População: Funcionários das empresas paraenses. Variáveis: Classe social, grau de instrução
(instituto consulplan 2023) Sabemos que um estudo estatístico pode ser feito com todos os elementos da população ou com uma parte desta população (amostra). Para que possamos usar os resultados obtidos na amostra para fazer inferências sobre a população de interesse, precisamos garantir que a amostra seja representativa desta população.
(FERREIRA, Valéria. Estatística Básica. Rio de Janeiro: SESES, 2015. Adaptado.)
Para obter uma amostra, pode-se utilizar diferentes técnicas de amostragem; analise-as.
I. Na amostragem aleatória simples, todos os elementos da população têm igual probabilidade de pertencer à amostra, assemelhando-se a um sorteio.
II. Na amostragem aleatória estratificada, os elementos da população são divididos em subgrupos (estratos) e é possível selecionar quantidades proporcionais de elementos de cada subgrupo.
III. Na amostragem sistemática, os elementos da população são organizados e ordenados; seleciona-se um número inicial aleatório, em seguida, os demais elementos são selecionados mantendo-se os intervalos regulares, a partir do número inicial.
Está correto o que se afirma em: I, II e III.
Amostragem casual simples: conhecida como amostragem ao acaso, aleatória ou randômica, sendo equivalente a um sorteio. Pode ser feita numerando a população e sorteando as amostras. Uma tabela de números randômicos pode ser um instrumento útil para realizar esse sorteio.
Amostragem sistemática: realizada em linhas de produção, onde são retirados elementos de forma sistemática e periódica para compor a amostra final. Por exemplo, a cada dez produtos produzidos, um é retirado e verificado. É uma amostragem fácil de ser realizada, mas podem ocorrer vícios na retirada da amostra. Tem melhor rendimento quando os indivíduos são ordenados por um critério que não tem relação com a medida de interesse.
Amostragem por conglomerados: é utilizada quando a população é dividida em pequenos grupos e a amostragem é feita por meio desses grupos, também chamados de conglomerados. Assim, o sorteio não é realizado dos elementos individuais da população, mas sim dos conglomerados.
Amostragem estratificada: para populações que são estratificadas e divididas em subpopulações (estratos) é possível que a variável estudada apresente um comportamento divergente entre as subpopulações, mas homogêneo dentro de cada uma das subpopulações. Assim, é importante considerar essas diferenças na escolha da amostra para que na amostra final não tenha mais representantes de um estrato do que de outro e inclua a mesma quantidade de representantes de cada estrato na amostra final. Pode ser usada a estratificação para sexo, idade, posicionamento geográfico, entre outros.
Fonte: Veludo AG, Araújo FM, Fernandez LR, Franco LF, Zuazo MAD, Gouveia VA. Tipos de Amostragem. Estudantes para as melhores evidências (EME) Cochrane. Disponível em: [colar link]. Acessado em [11, abr. e 2023]. https://eme.cochrane.org/tipos-de-amostragem/
(vunesp 2018) Considere as informações a seguir para construir uma distribuição de frequência sem intervalo de classe e responder a questão.
Um dado foi lançado 50 vezes e foram registrados os seguintes resultados:
5 4 6 1 2 5 3 1 3 3
4 4 1 5 5 6 1 2 5 1
3 4 5 1 1 6 6 2 1 1
4 4 4 3 4 3 2 2 2 3
6 6 3 2 4 2 6 6 2 1
A frequência simples absoluta do primeiro elemento é: 10.
A frequência absoluta simples corresponde ao número de observações correspondentes a uma determinada classe ou a um determinado valor, ou seja, o primeiro elemento "1" aparece 10 vezes.
A frequência absoluta é o número de vezes em que uma determinada variável assume um valor, enquanto a frequência relativa é o quociente entre a frequência absoluta da classe correspondente e a soma das frequências (total observado).
(vunesp 2013) Observe a tabela de distribuição de frequência a seguir onde xi é a variável estudada, fi é frequência absoluta, fa a frequência acumulada e fr a frequência relativa.
De acordo como os dados da tabela, ao se calcular o valor do terceiro quartil, verifica-se que: ele está localizado na classe que detém 27% dos dados.
Lembremos que um quartil é qualquer um dos três valores que divide o conjunto ordenado de dados em quatro partes iguais, e assim cada parte representa 1/4 da amostra ou população. Assim, no caso duma amostra ordenada,
primeiro quartil é o valor aos 25% da amostra ordenada.
segundo quartil (mediana) é o valor até ao qual se encontra 50% da amostra ordenada;
terceiro quartil é valor a partir do qual se encontram 25% dos valores mais elevados ou 75% da amostra ordenada.
Terceiro quartil = 3N/4 = 3*30/4= 90/4= 22.5.
Nesse caso, o fi que representa é o número 8, ou seja, está nesse intervalo. 8/30=26,6666 aproximadamente 27% da classe que detém os dados.
(cesgranrio 2010) O máximo de um gráfico de frequência absoluta acumulada de uma variável discreta é a(o): número total de observações.
A frequência absoluta acumulada em um gráfico mostra o número total de observações até um determinado ponto na distribuição. Portanto, quando atingimos o final do gráfico (máximo), o ponto mais alto representa o número total de observações coletadas.
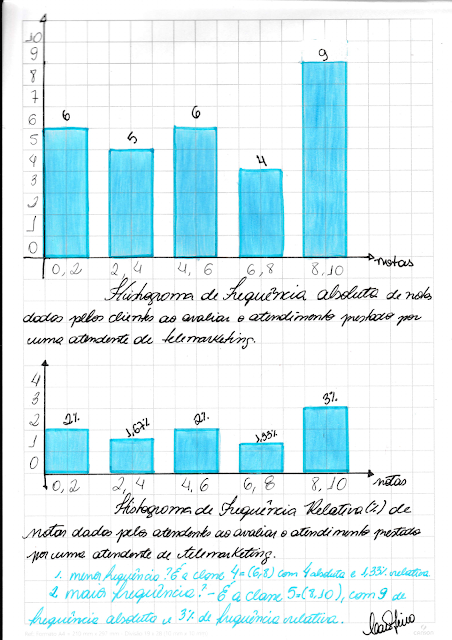
(consulplan 2023) O histograma, também conhecido como distribuição de frequências, é a representação gráfica em colunas ou em barras (retângulos) contíguas de um conjunto de dados previamente tabulado e dividido em classes equidistantes ou não. O eixo vertical do histograma pode ser construído a partir da frequência absoluta ou da densidade, definida como a frequência relativa da classe dividida pela amplitude da classe. Sobre a construção de um histograma, analise as afirmativas a seguir.
I. Se as classes são equidistantes, as formas dos histogramas construídos a partir da frequência absoluta e da densidade são equivalentes.
II. Em qualquer histograma, a classe modal é representada pela barra de maior altura.
III. No histograma construído a partir da densidade, a área do gráfico é igual a 1.
Está correto o que se afirma em: I e III, apenas.
II. Em qualquer histograma, a classe modal é representada pela barra de maior altura. Isso é geralmente verdade, mas não é uma regra absoluta. A classe modal é a classe com a maior frequência, o que geralmente corresponde à barra de maior altura em um histograma. No entanto, em casos de bimodalidade (duas classes com frequências muito semelhantes), pode haver duas barras de altura semelhante, representando duas classes modais. Portanto, a afirmativa é geralmente correta, mas há exceções.
(fepese 2013) Para a apresentação de dados estatísticos, podem-se utilizar histogramas de frequência simples ou absoluta, que são: Gráficos formados por um conjunto de retângulos justapostos, cujas bases se localizam sobre o eixo horizontal, de tal modo que seus pontos médios coincidam com os pontos médios dos intervalos de classe.
(cespe/cebraspe 2018) O histograma é um diagrama de retângulos contíguos com base na curtose das faixas de valores da variável e com área igual à diferença da frequência absoluta da respectiva faixa. ERRADO
Histograma é um gráfico de barras utilizado para representar a distribuição de uma variável. Ele não é baseado na curtose das faixas de valores, mas sim na frequência das observações em intervalos específicos. A curtose, por sua vez, é uma medida estatística que avalia a forma da distribuição dos dados em relação à normalidade. Ela não é diretamente utilizada na construção de histogramas. Portanto, o item está incorreto ao associar o histograma à curtose das faixas de valores. O histograma é construído com base nos valores observados e suas frequências, não na curtose.
(fundatec 2024) Em estatística básica, ao se analisar determinado conjunto de dados, consiste no resultado mais recorrente no conjunto, ou seja, com maior frequência absoluta. Trata-se da: Moda.
Moda é o valor que mais se repete/recorrente num determinado conjunto de dados.
(ibade 2018) Querendo saber o percentual de empregados por grau de instrução de uma empresa, um estatístico resolveu construir uma tabela de frequência absoluta dos empregados por nível de ensino e calcular a percentagem por grau de instrução destes empregados. Nesta perspectiva, assinale a alternativa correta em relação aos valores faltantes da tabela a seguir.
:0,1; 0,2; 0,27
Frequência absoluta total= 12+18+24+6+32+28 = 120
Porcentagem: 12/120=0,1; 24/120=0,2; 32/120= 0,26666 = 0,27.